Part A: Relative height[]
[]
Misc. Constants[]
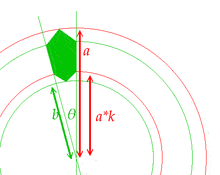
In the geometric facts article, we explained the construction of the "coin" which shows in Ep. 36 ~ Ep.48. Now we generalize it:
Let the Inner and the Outer ( of the construction circle ) be b and a, the middle red as K*a, the middle green as (1/K)*b. ( in the "coin"'s case, K=2/3 ). The angle as Theta.
Then the sum of the coin-shape area is:
This formula is much simpler then other shapes ( which constructed by these 4 circles ).
If we calculate the ratio between the "coin area" and the outer circle, we have: ( let the ratio be x )
Let Theta = 360 / v , we know it has:
So x is roughly ( 99.715~% when v = 24 ) :
MP: 1597 pixels; Chacha: 987 pixels
Now we know, only when K = 0.618033~, the golden ratio, then x can be (a / b)*v. This is the relation between the golden ratio and this kind of "shape" ( not the coin itself ).
We point out before that Magical Princess : Chacha is also 1 : 0.618~:
That's some supports that we claim the golden ratio as a "legit" constant in Akazukin Chacha.
There are also some constants we will use:
h = tan(360/7) = 1.25396034~
nearly 79/63 or (9^2-2)/(8^2-1)
y = 365.242199
A maybe misprinted Mahoujin[]
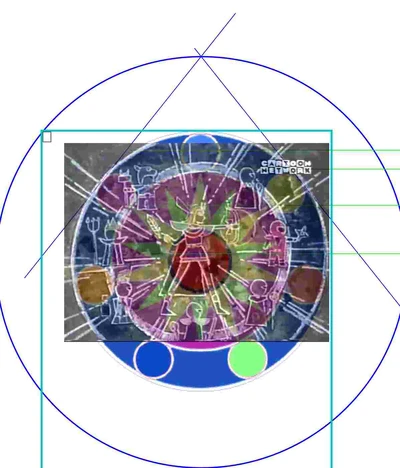
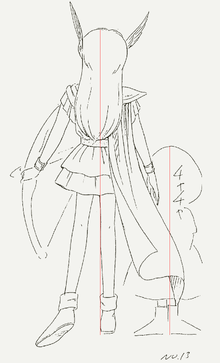
The Mahoujin formation shown on LD-13 ( DVD v2-6 ) conflicts with other displays in many ways, like the heptagon is not a regular one, the white rims overlaps each other ... etc. Early "researchers" of Akazukin Chacha like こっべ did not count it as a well-displayed one.
However, we still can see many properties of the normal one in this maybe "misprinted" one, like the Outer : Inner : P ( the yellow heptagram's ) = ratio. The rim and small circles may be just adjusted for better visual.
More we can see is, Magical Princess' arms are on the ( reversed ) heptagram, Chacha's feet touch the heptagon inside P circle. MP's height is as the diameter of the Outer Circle; Chacha's height is as the diameter of the inner deep green heptagram's circumcircle. ( That's said MP's is adjusted bigger of Chacha is adjusted smaller, and both are 2+ times lager then Ep.48,50's Mahoujin-Character ratio )
These are some reason we believe this formation still shows properties of Akazukin Chacha itself, although most are unclear by now. Despite of the geometric aspect, we can see MP and Chacha on LD13 cover can be linked with the Vitruvian Man Pose. In below we will see this ( the vitruvian-formation ) does exist in Akazukin Chacha itself.
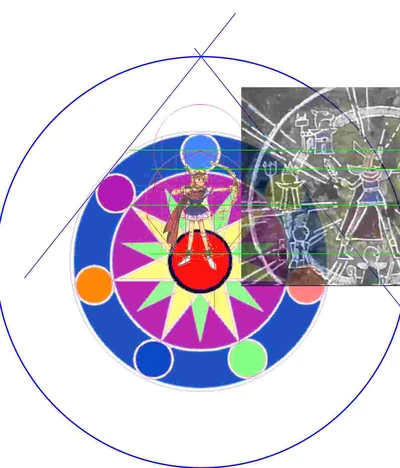
Vitruvian Man Formation and two supports of it[]

The animation below show the construction of the "base circle" and the "base square" of Vitruvian Man Formation ( of course Leonardo's, since we focus on its "natural" or mathematical properties, from Leonardo da Vinci or whoever is irrelevant ) form a heptagon. This was originally used to explain MP's "eidos / idea of human" role. We can see the relations between her body parts or costume with those lines.
The thing we want to bring out from this formation is: the "base circle", which is 2*0.618~ times of the height of MP.
First, in Ep. 48, the "Inner" and "Outer" of the "mural Mahoujin" is same as the normal Mahoujin ( both are 1 : sqrt(2) ) as the pic below:
And we know MP's height is equal to the radius of Inner. In below, we align MP and the exaggerated-art-style Mural MP / Joan I , and we can see the top of the "base circle" of MP is just at the same horizont of the Mural one's head.
In the pic below, we expand the base circle to a 1:tan(2pi/7) rectangle:
Between two black lines is that rectangle.
Let the short side of the rectangle.( = 2*[MP's height]/φ ) be k, then k* is the short side of the green rectangle. The width of the pic is also multiply with the long side of the green rectangle.
Thus the area of the Blue-Shaded Ellipse is equal to the area of Green Rectangle. (since divided by )
We know MP's height = 365.2421990741 MA/2 ( see below ), thus we can find that the red diagonal in the Green Rectangle is about 346.62007~, aka an Eclipse Year (aka Draconic Year) by days.
We now put the 8x7 grid from ED3 inside the green rect. :
The white borders between the screenshot and the green rect is to pad ( un-crop ) the screenshot to actual 8x7 blocks.
We know the short side of each small blocks is equal to [Chacha's height]/4 ( ignore perspective ). the quarter of [Chacha's height] is also the diameter of Coins' Format (see Geometric Fact article).
The area of each small blocks is 300*pi MA^2.

Cel and actual screenshot, cropped area.
We'll call the Green Rect. the True Screen afterward, and assume every screen from Akazukin Chacha anime was cropped from the True Screen to fit the real-world television standards.
We call the 1:tan(2pi/7) rect. A, and the green rect. B, then we have the length value chart below:
| Accurate value = | Rounded + | (1/μ) |
|---|---|---|
| part | Rounded value | μ |
| A long | 1132 | +3.986097 |
| A short | 903 | -16.65 |
| B short | 800 | +4.7690164 |
All of these values are 4 times bigger then actual value.
...editing...
Part B: Length Unit MA and Character's heights in value[]
MA can be represented as MAGIKana :
.If the system allows, we may replace MA with the char above.
1 MA = 0.943 Cm or 33/35 Cm
Let the diameter of Mahoujin's inner circle be 365.2421990741 (We mentioned this number on the Geometric Fact article ), then we have:
MP(equal to the radius of the inner circle) = 182.62MA = 172.19Cm
Chacha (MP/φ) = 112.87MA = 106.42Cm
Yanchuu and other early researchers like Clishna uses 1M as Chacha's height, (see here)
Our result (106.4 cm) does not have big conflict to theirs.
We have several supports form the Official Setting, one is the trumpet from Ep. 43 ( normal length of a trumpet is about 56 cm ), the two is the Indian rhinoceros from Ep. 13 ( one-horned rhinoceros, which normal shoulder height is about 1.85 m ).
Now we see into those numbers. We know a tropical year is the 365.2421990741 (days) we mentioned above, and a tropical month is 1530/56 (days). We have:
33/35 = 56*[tropical month]/[tropical year]*sqrt(2)*pi
The accuracy of this is amazingly high (99.999934%).
Since the [tropical year] or 365.242199~ is the diameter of the inner circle,that means
In Mahoujin inner-outer circles format, when the diagram of inner is a [tropical year] in MA, then the circumference of the outer is 56 (7x8) times of [tropical month] in Cm.
Also this: ((sqrt(2)-1)*365.242199~*0.943(or 33/35)/4)^2*pi is about 4000,
that's said the area of each "seven small circles" ( include the rim ) is about 4000 cm^2.
Another interesting thing is, make Chacha's height as a circle's diameter, then the area of that circle is about
10000 MA^2. ((365.242199~*(sqrt(5)-1)/8)^2*pi) =10004.9~
That circle is just the 3rd central circle.
Now we have the area of whole Mahoujin ( inclue the white rim of the outer ):
([tropical year in MA]*sqrt(2)*(57/55)/2)^2*pi = (4^2)*12500 cm^2 approximately.
12500 can be 50000/4. The error of these three are all about 5 cm^2 or 5 MA^2.
The quarter of the radius of Mahoujin (include white rim) is close to radius of the white rim of 1st central circle (the cos(3pi/7)/cos(2pi/7) one )
reminder
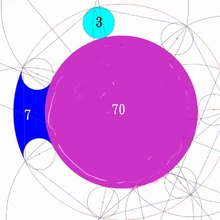
We said the inner circle. : small circle : semi-fan-shaped area = 70 : 3 : 7 approximately before. Now we can see the Greatest Common Divisor of this is
1500 MA^2 ( this's also a N*10^n ( N and n are integers from 1 to 9 ) type number divide by 2 )
Thus the inner circle is about 70*1500 MA^2 (99.89%); the small circle is about 3*1500 MA^2 (99.87%).
(Quasi) Imperial Units and MA[]
It's said that one Inch is equal to [one degree of arc along the equator]/([tropical year]*12*10^3) cm. ( see Robin Heath, SUN, MOON & EARTH ).
With the relation of MA and cm Akazukin Chacha shows by itself, we can find a quasi-Inch which close to real world Inch.
First, we set the accurate value of 56*[tropical month] to (13770.07731)/9 ( this's not only a "palindromic" number, but also the accurate value of 56 tropical month, 56* 27d7h43m4.682s )
Make a rectangular triangle with 35 cm wide and 35 MA high ( thus the height is actually 33.000163657~ cm),
then we define the length of the hypotenuse to 19 (quasi-) Inch.
Thus a (quasi-) Inch is about 2.53179~ cm.
Put this value back to the [one degree of arc along X ]/([tropical year]*12*10^3) formula ( X is a circle with radius R ), we can see the R is equal to 6357.9 KM, in other word the polar radius of Earth. ( The 6358 value actually used in GPS or Map projection. Try search 6358+earth+radius on google)
That's said the X is the vertical circle of Earth, we call the value 2.53179~ cm.a quasi-Inch since it relates to the real world Inch definition ( and the Earth itself ).
The interesting thing of this is the height of both Chacha and MP are almost integers in this q-Inch unit:
Chacha = 42.0322~ q-inch = 3'6''q-ft
MP = 68.0095~ q-inch = 5'8''q-ft
...editing...